| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 판교퇴근길밋업
- ai개발밋업
- 부스트캠프 AI Tech
- homebrew설치
- CNN
- 리눅스연습문제
- Django
- MAC OS
- 2020정보처리기사
- 우분투리눅스
- BPTT
- Swing
- backpropagation
- github branch
- 딥러닝
- 쉽게배우는운영체제
- Git
- RNN
- java
- 운영체제연습문제
- 정보처리기사
- AIStages
- Python
- 운영체제
- 파이썬
- 자바
- 애드센스
- ann
- GitHub
- 워드프레스
- Today
- Total
코딩하는 애옹😸
(AI Math 7강) 통계학 맛보기 본문
통계학
통계적 모델링의 목표 : 적절한 가정 위에서 확률분포를 추정(inference)
근사적으로 확률분포를 추정
(예측모델의 목적 : 분포를 정확하게 맞추는 것 X, 예측의 위험을 최소화)
- 모수적(parametric) 방법론
- 데이터가 특정 확률분포를 따른다고 선험적(a priori)으로 가정한 후 그 분포를 결정하는 모수(parameter)를 추정
- 비모수(nonparametric) 방법론
- 특정 확률분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀜
- 기계학습의 많은 방법론은 비모수에 속함
예제
확률분포를 가정하는 방법: 히스토그램 모양 관찰
- 데이터가 2개의 값(0또는 1)만 가지는 경우 : 베르누이분포
- 데이터가 n개의 이산적인 값을 가지는 경우 : 카테고리분포
- 데이터가 [0,1]사이에서 값을 가지는 경우 : 베타분포
- 데이터가 0 이상의 값을 가지는 경우 : 감마분포, 로그정규분포 등
- 데이터가 R전체에서 값을 가지는 경우 : 정규분포, 라플라스분포 등
데이터를 생성하는 원리부터 고려
데이터의 확률분포를 가정했다면 모수를 추정할 수 있음
정규분포의 모수 : 평균 $\mu$과 분산 $\sigma^2$
이를 추정하는 통계량(statistic)
- 표본평균 $\bar{X}$ : 주어진 데이터들의 산술평균
- 표본평균의 기댓값 $\mathbb{E}[\bar{X}]$ : 원래 데이터의 평균과 같음
- 표본분산 $S^2$ : 주어진 데이터에서 표본평균을 뺀 값을 제곱한 후 산술평균
(N대신 N-1개로 나눔 : 불편(unbiased)추정량을 구하기 위함, 기대값을 취했을 때 원래 모집단에 일치하는 것을 목표로 하기 위함) - 표본분산의 기댓값 $\mathbb{E}[S^2]$ : 원래 데이터(모집단)의 분산과 같음
표집분포(sampling distribution): 통계량의 확률분포
- 표본평균의 표집분포는 $N$(데이터)이 커질수록 정규분포를 따름 : 중심극한정리(Central Limit Theorem)
최대가능도 추정법(maximum likelihod estimation, MLE)
확률분포마다 사용하는 모수가 다르므로 적절한 통계량이 달라짐
따라서 이론적으로 가장 가능성이 높은 모수를 추정하는 방법 이용

- 가능도(likelihood)함수 : $L(\theta;x)$
- 모수 $\theta$를 따르는 분포가 $x$를 관찰할 가능성을 뜻하지만 확률로 해석x
- 데이터가 주어져있는 상황에서 $\theta$를 변형함에 따라 값이 바뀌는 함수
- 데이터 집합 $X$가 독립적으로 추출되었을 경우 로그가능도를 최적화

- 확률질량(밀도)함수들의 누적곱으로 표현
- 양변의 로그를 씌우면 로그가 곱을 덧셈으로 바꿔줌
- 로그가능도를 쓰는 이유? 컴퓨터 연산 정확도를 위해
- 경사하강법으로 가능도를 최적화할 때 미분 연산 사용 -> 로그가능도를 사용하면 연산량을 $O(n^2)$를 $O(n)$으로 줄임
예제 (정규분포)
정규분포를 따르는 확률변수 $X$로부터 독립적인 표본 {$x_1, ... ,x_n$}을 얻었을 때 최대가능도 추정법을 이용하여 모수를 추정하면?

- $\mu$와 $\sigma$로 미분한 후 각 식이 0이 되는 $\mu$, $\sigma$를 찾으면 가능도를 최대화
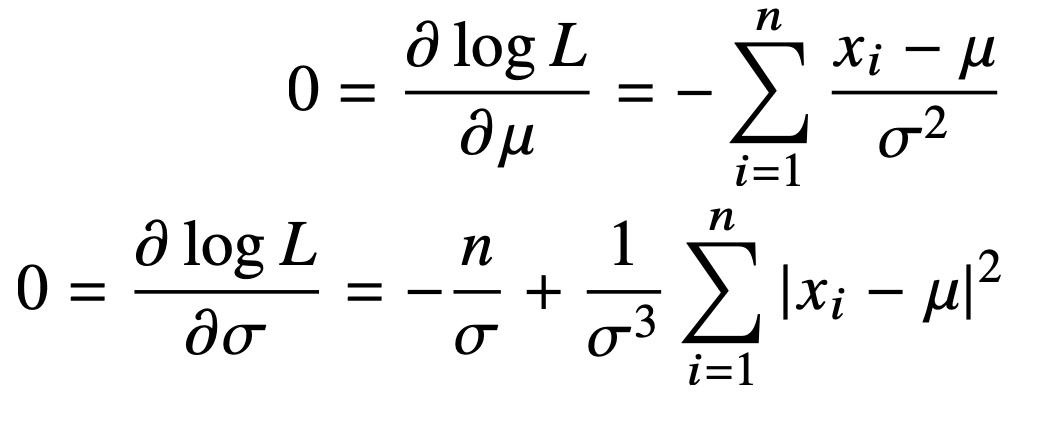
결론)
예제 (카테고리분포)
카테고리 분포 Multinoulli($x;p_1,...,p_d$)를 따르는 확률변수 $X$로부터 독립적인 표본 {$x_1, ... ,x_n$}을 얻었을 때 최대가능도 추정법을 이용하여 모수를 추정하면?
카테고리분포 : 베르누이 분포(두개의 값 중 하나를 선택하는 확률분포)의 다차원($d$)으로 확장하는 개념
$x$ : one-hot 벡터로 표현됨
모수 $P_k$ : $P_{1~d}$의 각각의 차원에서 1또는 0이 될 확률 = 다 더했을 때 1
모수에 주어진 데이터 $X_i$의 $k$번째 차원을 승수를 취함
- $x_{i,k}$ 가 0이 되면 $P_k^{x_{i,k}}$ = 1
$N_k$ : 주어진 각 데이터$x_i$에 대해서 $k$값이 1 갯수를 카운팅


라그랑주 승수법을 이용
- 제약식의 등식을 양변으로 넘겨준 후, $\lambda$를 곱해준 것을 본 식에 더함
-> 목적식 최적화, 제약식도 만족하면 주어진 로그가능 최대하는 $P_{1..k}$를 구할 수 있음
- $n_k (k=1..d)$ : 데이터 갯수
- 카테고리 분포에서 MLE는 경우의 수를 세어서 비율을 구하는 것, 각각의 차원에 해당하 데이터의 숫자
- 제약식의 등식을 양변으로 넘겨준 후, $\lambda$를 곱해준 것을 본 식에 더함
딥러닝 모델의 가중치를 $\theta = (W^{(1)},...,W^{(L)})$라고 표기했을 때,
분류 문제에서 softmax벡터는 카테고리 분포의 모수 $(p_1,...,p_k)$를 모델링
one-hot벡터로 표현한 정답레이블 $y = (y_1,...,y_k)$을 관찰데이터로 이용해 확률분포인 softmax벡터의 로그가능도를 최적화
확률분포의 거리
손실함수 : 모델이 학습하는 확률분포와 데이터에서 관찰되는 확률분포의 거리를 통해 유도
데이터 공간에 두 개의 확률분포 $P(x), Q(x)$가 있을 경우
- 총변동 거리 (Total Variation Distance, TV)
- 쿨백-라이블러 발산 (Kullback-Leibler Divergence, KL)
- 바슈타인 거리 (Wasserstein Distance)
쿨백-라이블러 발산 (KL-Divergence)

분해하면
- 분류 문제에서 정답레이블을 $P$, 모델 예측을 $Q$라 두면 MLE는 KL-Divergence를 최소화하는 것과 같다
'부스트캠프 AI Tech 3기 > Study' 카테고리의 다른 글
| (AI Math 9강) CNN (0) | 2022.01.21 |
|---|---|
| (AI Math 8강) 베이즈 통계학 (0) | 2022.01.20 |
| (AI Math 6강) 확률론 맛보기 (0) | 2022.01.18 |
| (AI Math 5강) 딥러닝 학습방법 이해하기 (0) | 2022.01.18 |
| (AI Math 3~4강) 경사하강법 (0) | 2022.01.17 |
