| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 운영체제
- java
- 쉽게배우는운영체제
- BPTT
- GitHub
- MAC OS
- 정보처리기사
- 운영체제연습문제
- AIStages
- ann
- 애드센스
- homebrew설치
- backpropagation
- 자바
- 부스트캠프 AI Tech
- Django
- 워드프레스
- github branch
- RNN
- Python
- Git
- 우분투리눅스
- 리눅스연습문제
- 파이썬
- 2020정보처리기사
- CNN
- ai개발밋업
- 딥러닝
- Swing
- 판교퇴근길밋업
- Today
- Total
코딩하는 애옹😸
(AI Math 9강) CNN 본문
CNN
커널 V를 입력벡터 x 상에서 움직여가며 선형모델과 합성함수 적용
$$
h_i = \sigma\left( \sum_{j=1}^{k}V_jx_{i+j-1} \right)
$$
- $\sigma$ : 활성함수
- $V_j$ : 가중치 행렬 = 커널(은 변하지 않음)
- $k$ : 커널 사이즈
Convolution 연산
커널을 이용해 신호(signal)를 국소적으로 증폭 또는 감소시켜서 정보를 추출 또는 필터링하는 것
(신호 g, 커널 f, 엄밀히 말하면 x-z 대신 x+z -> cross-correlation)
- 연속
$$
[f*g](x) = \int_{\mathbb{R}^d}f(z)g(x-z)\, dz = \int_{\mathbb{R}^d}f(x-z)g(z)\, dz = [g*f](x)
$$
- 이산
$$
[f*g](i) = \sum_{a\in\mathbb{Z}^d}f(a)g(i-a) = \sum_{a\in\mathbb{Z}^d}f(i-a)g(a) = [g*f](i)
$$
다양한 차원에서의 Convolution
1D-conv
$$
[f*g](i) = \sum_{p=1}^{d}{f(p)g(i+p)}
$$2D-conv
$$
[f*g](i,j) = \sum_{p,q}^{d}{f(p,q)g(i+p,j+q)}
$$3D-conv
$$
[f*g](i,j,k) = \sum_{p,q,r}^{d}{f(p,q,r)g(i+p,j+q,k+r)}
$$
2차원 Convolution 연산
입력 크기 $(H,W)$, 커널 크기 $(K_H,K_W)$, 출력 크기 $(O_H,O_W)$
$$
O_H = H - K_H +1\\
O_W = W - K_W + 1
$$
Convolution 연산의 역전파
입력부분에 미분이 적용 -> g'와 f의 convolution 연산
그림으로 쉽게 이해하자!
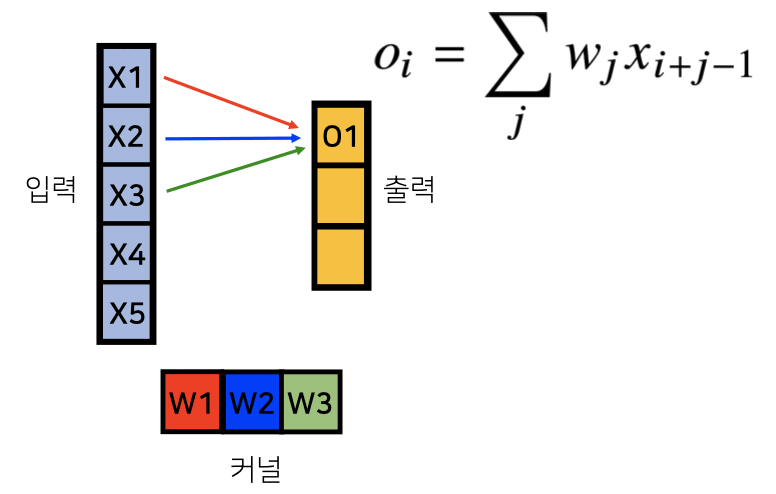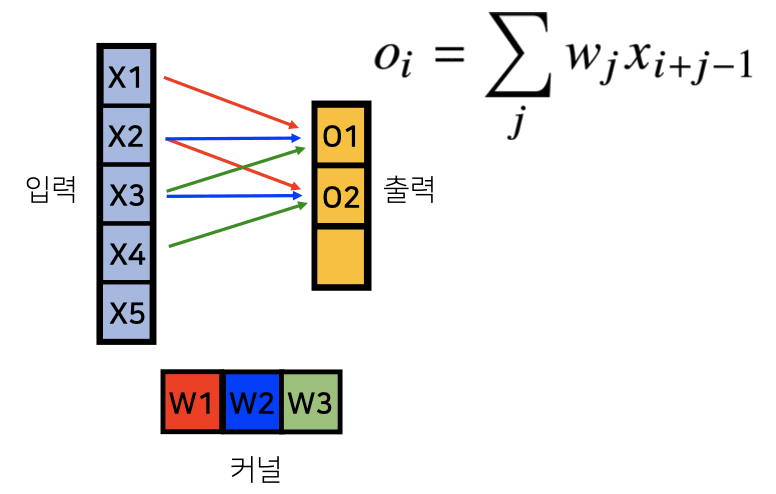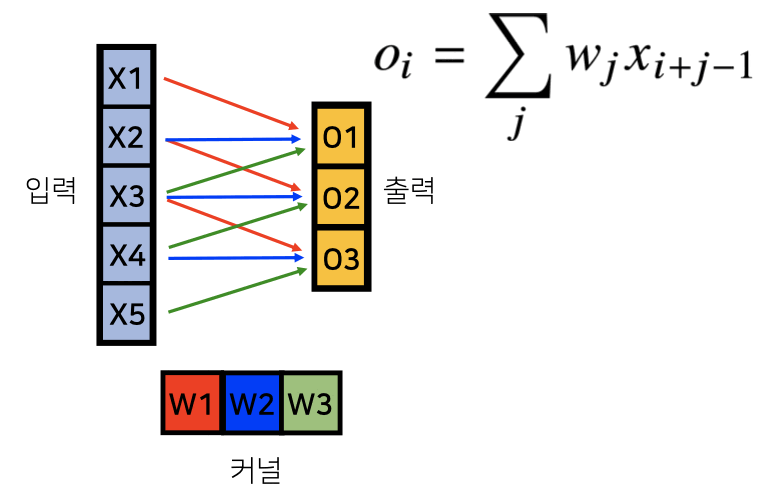
[그림] convolution 연산
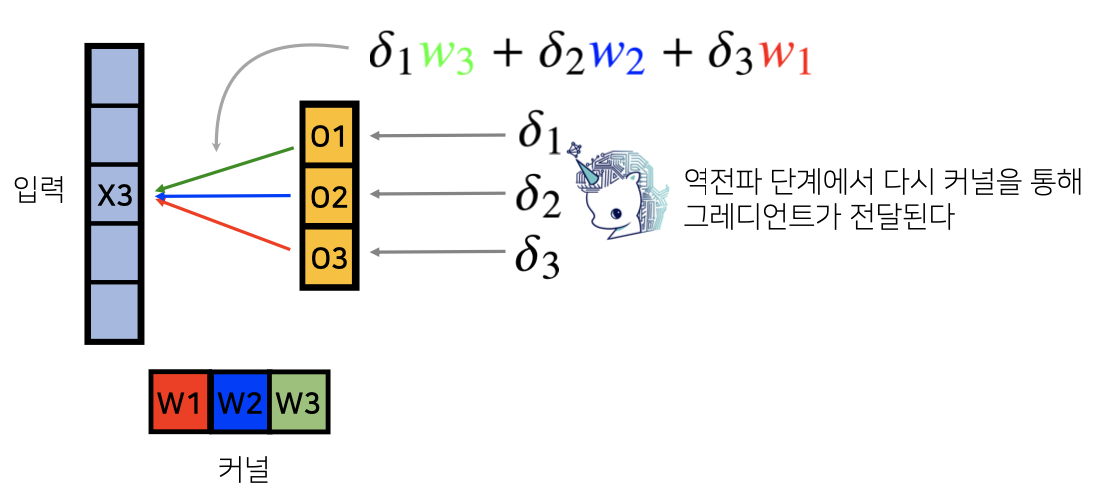
[그림] 역전파 ($\delta$는 미분값)
- 입력벡터는 곱해졌던 커널들을 통해 그래디언트 전달

[그림] 역전파
- $o_3$에서 $\delta_3$는 $w_1$을 통해서 그래디언트를 전달했기 때문에, $\delta_3$를 $w_1$으로 배당, $w_1$대신 $x_3$를 곱해서 $w_1$의 그래디언트가 됨
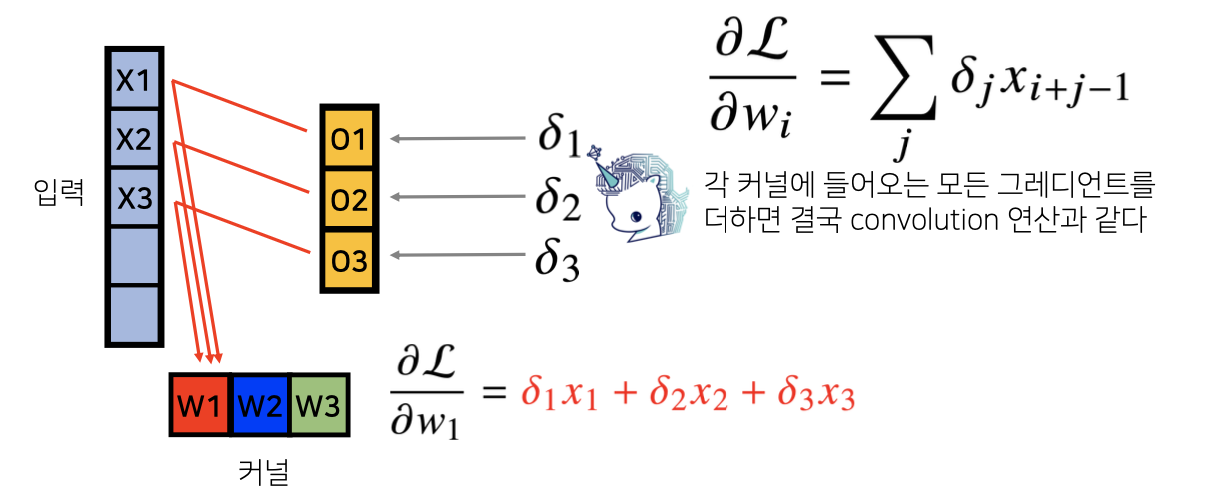
[그림] 결과
'부스트캠프 AI Tech 3기 > Study' 카테고리의 다른 글
| [예제] BackPropagation (0) | 2022.01.23 |
|---|---|
| (AI Math 10강) RNN (0) | 2022.01.21 |
| (AI Math 8강) 베이즈 통계학 (0) | 2022.01.20 |
| (AI Math 7강) 통계학 맛보기 (0) | 2022.01.20 |
| (AI Math 6강) 확률론 맛보기 (0) | 2022.01.18 |
