| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 리눅스연습문제
- 딥러닝
- 워드프레스
- Django
- 판교퇴근길밋업
- 운영체제연습문제
- Python
- RNN
- Git
- 자바
- 쉽게배우는운영체제
- homebrew설치
- 파이썬
- CNN
- 부스트캠프 AI Tech
- github branch
- 애드센스
- MAC OS
- 2020정보처리기사
- backpropagation
- Swing
- ann
- 정보처리기사
- 운영체제
- java
- AIStages
- ai개발밋업
- 우분투리눅스
- GitHub
- BPTT
- Today
- Total
코딩하는 애옹😸
[예제] BackPropagation 본문
계산 과정
- 순전파 과정을 통해 예측값과 실제값의 오차 구하기
- 오차를 구한 후, 역전파를 이용하여 가중치($w_n$)업데이트
- 업데이트된 가중치를 이용하며 다시 순전파 계산
- 업데이트된 오차 확인
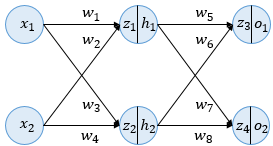
주어진 조건
- $x_1$ = 0.1, $x_2$ = 0.2
- {$w_1, w_2, ... , w_8$} = {0.3, 0.25, 0.4, 0.35, 0.45, 0.4, 0.7, 0.6}
- 실제 값 : 0.4 , 0.6
- 활성화 함수 $\sigma$ : $sigmoid$함수 $$sigmoid(x) = \frac{1}{1+e^{-x}}$$
1. 순전파
$z_1 = x_1\cdot w_1 + x_2\cdot w_2$
$z_2 = x_1\cdot w_3 + x_2\cdot w_4$
이때, $h_1$과 $h_2$는 $z_1$과 $z_2$를 은닉층의 활성화함수에 계산하여 출력된다.
$h_1 = \sigma(z_1) = sigmoid(z_1)$
$h_2 = \sigma(z_2) = sigmoid(z_2)$
$z_3$와 $z_4$는 각각 $h_1$과 $h_2$에 가중치를 곱하고 다시 활성화함수를 이용하면 예측값 $o_1$, $o_2$를 구할 수 있다.
$z_3 = h_1\cdot w_5 + h_2\cdot w_6$
$z_4 = h_1\cdot w_7 + h_2\cdot w_8$
$o_1 = \sigma(z_3) = sigmoid(z_3)$
$o_2 = \sigma(z_4) = sigmoid(z_4)$
여기서 예측값과 실제값의 오차($E$)를 구하기 위해서 오차제곱합의 평균(MSE, L2 loss)을 이용한다.
$E_{o_1} = \frac{1}{2}(0.4 - o_1)^2$
$E_{o_2} = \frac{1}{2}(0.6 - o_2)^2$
$E = E_{o_1} + E_{o_2}$
2. 역전파 (BackPropagation)
먼저, 4개의 가중치 ($w_5, w_6, w_7, w_8$)를 미분의 연쇄법칙을 이용하여 업데이트한다.
$$
\frac{\partial{E}}{\partial{w_5}} = \frac{\partial E}{\partial o_1}\times \frac{\partial o_1}{\partial z_3}\times \frac{\partial z_3}{\partial w_5}
= -(0.4 - o_1)\times sigmoid(z_3)(1-sigmoid(z_3))\times h_1 \rightarrow w_5^{+}
$$
위와 같은 방법으로 $w_6, w_7, w_8$도 업데이트한다.
$
\frac{\partial{E}}{\partial{w_6}} = \frac{\partial E}{\partial o_1}\times \frac{\partial o_1}{\partial z_3}\times \frac{\partial z_3}{\partial w_6} \rightarrow w_6^{+}
$
$
\frac{\partial{E}}{\partial{w_7}} = \frac{\partial E}{\partial o_2}\times \frac{\partial o_2}{\partial z_4}\times \frac{\partial z_4}{\partial w_7} \rightarrow w_7^{+}
$
$
\frac{\partial{E}}{\partial{w_8}} = \frac{\partial E}{\partial o_2}\times \frac{\partial o_2}{\partial z_4}\times \frac{\partial z_4}{\partial w_8} \rightarrow w_8^{+}
$
이제 $w_1, w_2, w_3, w_4$를 업데이트한다.
$w_1$를 업데이트하기 위해서는 $\frac{\partial E}{\partial{w_1}}$ 를 계산해야한다.
$$\frac{\partial E}{\partial{w_1}} = \frac{\partial E}{\partial{h_1}}\times \frac{\partial h_1}{\partial z_1}\times \frac{\partial z_1}{\partial w_1} \rightarrow w_1^{+} $$
여기서 $\frac{\partial E}{\partial h_1} = \frac{\partial E_{o_1}}{\partial h_1} + \frac{\partial E_{o_2}}{\partial h_1}$ 와 같이 풀어쓸 수 있다.
$\frac{\partial E_{o_1}}{\partial h_1} = \frac{\partial E_{o_1}}{\partial z_3}\times \frac{\partial z_3}{\partial h_1} = \frac{\partial E_{o_1}}{\partial o_1}\times \frac{\partial o_1}{\partial z_3} \times \frac{\partial z_3}{\partial h_1}$
$\frac{\partial E_{o_2}}{\partial h_1} = \frac{\partial E_{o_2}}{\partial z_4}\times \frac{\partial z_4}{\partial h_1} = \frac{\partial E_{o_2}}{\partial o_2}\times \frac{\partial o_2}{\partial z_4} \times \frac{\partial z_4}{\partial h_1}$
위와 같은 방법으로 $w_2^{+}, w_3^{+}, w_4^{+} $를 모두 구할 수 있다.
$
\frac{\partial E}{\partial{w_2}} = \frac{\partial E}{\partial{h_1}}\times \frac{\partial h_1}{\partial z_1}\times \frac{\partial z_1}{\partial w_2} \rightarrow w_2^{+}
$
$
\frac{\partial E}{\partial{w_3}} = \frac{\partial E}{\partial{h_2}}\times \frac{\partial h_2}{\partial z_2}\times \frac{\partial z_2}{\partial w_3} \rightarrow w_3^{+}
$
$
\frac{\partial E}{\partial{w_4}} = \frac{\partial E}{\partial{h_2}}\times \frac{\partial h_2}{\partial z_2}\times \frac{\partial z_2}{\partial w_4} \rightarrow w_4^{+}
$
3. 순전파
업데이트된 가중치 $w_{n}^{+}$로 다시 예측값을 구해서 오차를 계산한다.
[1. 순전파]와 같은 방법 이용한다.
편의를 위해 숫자를 대입한 계산을 생략하였다.
숫자를 대입하여 계산하면 역전파를 이용한 오차값이 더 작아졌다는 것을 알아 낼 수 있다.
끝.
(오타 지적 환영)
'부스트캠프 AI Tech 3기 > Study' 카테고리의 다른 글
| [PyTorch] AutoGrad (0) | 2022.01.25 |
|---|---|
| [PyTorch] Basics (0) | 2022.01.25 |
| (AI Math 10강) RNN (0) | 2022.01.21 |
| (AI Math 9강) CNN (0) | 2022.01.21 |
| (AI Math 8강) 베이즈 통계학 (0) | 2022.01.20 |
